Công thức tính diện tích hình bình hành, chu vi và bài tập vận dụng

Diện tích hình bình hành là chương trình học có trong Toán học 4 và được tìm hiểu chi tiết hơn trong chương trình Toán học THCS. Nếu như bạn chưa nắm chắc các công thức tính chu vi, diện tích của hình bình hành thì đừng bỏ lỡ nội dung thông tin có trong bài viết chi tiết dưới đây.

Hình bình hành là hình gì?

Hình bình hành là tứ giác mà có 2 cặp cạnh đối song song với nhau hoặc 1 cặp cạnh đối song song và bằng nhau. Trong hình bình hành sẽ có 2 góc đối bằng nhau, 2 đường chéo cắt nhau tại trung điểm của hình.

Thực chất, hình bình hành là trường hợp đặc biệt của hình thang. Trong đó:

• Hình thang có 2 cạnh đáy bằng nhau được gọi là hình bình thành
• Hình thang có 2 cạnh song song thì đó là hình bình hành.

Dấu hiệu nhận biết của hình bình hành

Có 5 dấu hiệu nhận biết của hình bình hành, đó là:

• Tứ giác mà có các cạnh đối song song với nhau
• Tứ giác có các cạnh đối bằng nhau
• Tứ giác có 2 đường chéo cách nhau tại trung điểm của mỗi đường
• Tứ giác được tạo nên bởi 2 cạnh đối song song và bằng nhau
• Tứ giác được tạo bởi 2 góc đối bằng nhau.

Tính chất của hình bình hành

• Hình bình hành là tứ giác có các góc đối bằng nhau
• Các cạnh đối trong hình bình hành luôn song song với nhau
• Hai đường chéo của hình bình hành sẽ cắt nhau tại trung điểm của mỗi đường

Xem thêm: Công thức tính thể tích hình lập phương, diện tích và bài tập

Các công thức hình bình hành

Công thức tính chu vi hình bình hành

Cách tính chu vi hình bình hành khá đơn giản, bạn chỉ cần áp dụng đúng công thức sau: C = (a+b) x 2

Trong đó:

• C: Là chu vi
• a và b: Là 2 cạnh nằm kề nhau của hình bình hành.

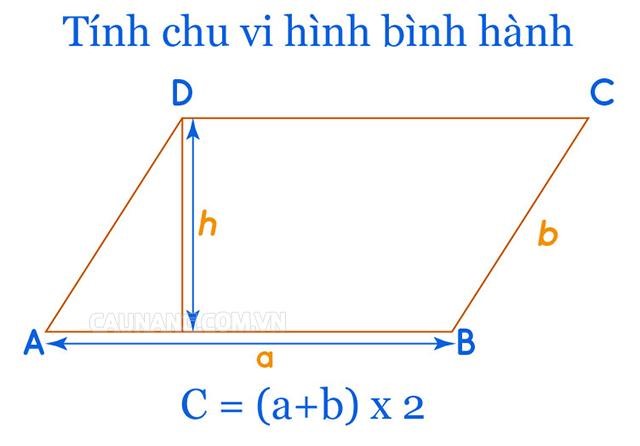
Chu vi hình bình hành là tổng độ dài của 4 cạnh hình bình hành, hay nói cách khác bằng 2 lần tổng một cặp cạnh của hình bình hành đó.

Công thức tính diện tích hình bình hành

Diện tích hình bình hành là toàn phần mặt phẳng ta có thể nhìn thấy được. Diện tích hình bình hành sẽ được tính theo công thức tích của cạnh đáy nhân với chiều cao. Công thức diện tích hình bình hành như sau: S = a.h

Trong đó:

• S: Là diện tích
• a: Là cạnh đáy
• h: Là chiều cao của hình bình hành.

Cách tính diện tích hình bình hành khi biết 2 đường chéo

Công thức tính hình bình hành khi biết 2 đường chéo đó là S= 1/2 .c.d.sinα

Trong đó:

• c, d: Là độ dài của 2 đường chéo hình bình hành (Có cùng đơn vị đo)
• α: Là góc tạo bởi 2 đường chéo

Cách nhớ công thức tính chu vi, diện tích hình bình hành

Phương pháp học: Thường xuyên làm bài tập vừa giúp thành thạo các phép toán, ghi nhớ công thức, hiểu kỹ hơn về vấn đề. Hơn nữa còn giúp việc tư duy, giải quyết vấn đề tốt hơn.

Mẹo nhớ công thức: Câu thơ về công thức tính diện tích, chu vi hình bình hành

Bình hành diện tích tính sao

Chiều cao nhân đáy ra liền khó chi

Chu vi thì cần những gì

Cạnh kề cộng lại ta liền nhân hai

Xem thêm: Tam giác đều là gì? Công thức tính chu vi và diện tích tam giác đều

Một số bài tập về tính diện tích, chu vi hình bình hành

Bài tập 1: Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5, chiều dài CD là 10, hãy tính diện tích hình bình hành ABCD.

Gợi ý đáp án:

S (ABCD) = 5 x 10 = 50 cm²

Bài tập 2: Cho hình bình hành có chu vi là 364cm và độ dài cạnh đáy gấp 6 lần cạnh kia; gấp 2 lần chiều cao. Tính diện tích hình bình hành.

Gợi ý đáp án:

• Nửa chu vi hình bình hành là: 364 : 2 = 182 (cm)
• Cạnh đáy gấp 6 lần cạnh kia nên nửa chu vi sẽ gấp 7 lần cạnh kia.
• Cạnh đáy hình bình hành là: 182 : 7 x 6 = 156 (cm)
• Chiều cao hình bình hành là: 156 : 2 = 78 (cm)
• Diện tích hình bình hành là: 156 x 78 = 12168 (cm²)

Bài tập 3: Cho hình bình hành ABCD với chu vi bằng 28cm. Với độ dài cạnh cạnh đáy bằng 3/4 độ dài cạnh còn lại và bằng độ dài chiều cao (h). Hãy tính diện tích hình bình hành ABCD.

Gợi ý đáp án:

Gọi độ dài cạnh đáy = a 

Ta có: độ dài chiều cao h = a 

=> Độ dài cạnh còn lại = 3/4a

Chu vi hình bình hành = 2.(a+b) = 28 cm = 2.(a + 3/4a) = 2.7/4a = 28 ⇔ a = 8 cm

Độ dài cạnh còn lại = 3/4a = 6cm 

Độ dài chiều cao h = a = 8cm

=> Diện tích hình bình hành ABCD = a.h = 8.8 = 64cm²

Với các thông tin trên đây về chu vi, diện tích hình bình hành, hy vọng sẽ giúp ích bạn. Để tìm hiểu nhiều công thức toán học hữu ích khác, quý bạn đọc hãy truy cập website caunang.com.vn