–>

Tam giác đều là gì? Công thức tính chu vi và diện tích tam giác đều

Posted On By Hoangcuc Posted in Tin Tức

Bên cạnh tam giác vuông, tam giác cân,… thì tam giác đều cũng là một chương trình học quan trọng, xuất hiện rất nhiều trong các bài thi học kì. Vậy tam giác đều là gì? Công thức tính chu vi và diện tích như thế nào? Tất cả sẽ có trong nội dung bài viết dưới đây của caunang.com.vn!

Tam giác đều là gì? Định nghĩa tam giác đều

Tam giác đều là tam giác có ba cạnh bằng nhau hoặc có ba góc bằng nhau và bằng 60°. Nói cách khác, tam giác đều là một đa giác đều có số cạnh bằng 3.

Tính chất của tam giác đều

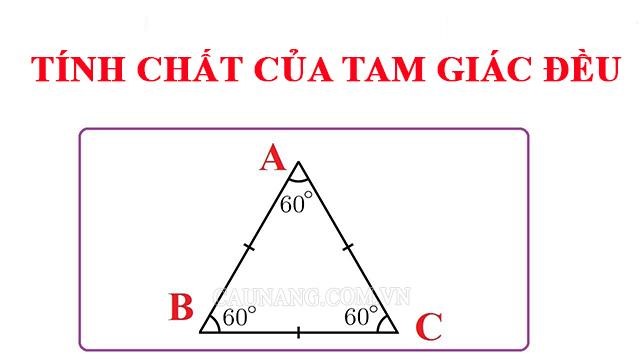
Tam giác đều

  • Trong một tam giác đều, mỗi góc sẽ bằng 60°. Tam giác ABC đều =>
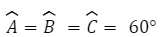
  • Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. Nếu góc A = góc B = góc C thì tam giác ABC đều.
  • Nếu một tam giác cân có 1 góc bằng 60° thì tam giác đó là tam giác đều. Tam giác ABC cân tại A, có góc A = 60° hoặc góc B = 60° hoặc góc C = 60°, thì tam giác ABC đều.
  • Trong tam giác đều, đường trung tuyến của tam giác sẽ là đường cao và sẽ là đường phân giác của tam giác đó. Tam giác ABC có AD là đường trung tuyến kẻ từ đỉnh A, khi đó AD là đường cao, đường phân giác của tam giác ABC.

Dấu hiệu nhận biết tam giác đều

Từ định nghĩa tam giác đều bạn dễ dàng nắm chắc được các dấu hiệu nhận biết, đó là:

  • Tam giác có 3 cạnh bằng nhau sẽ là tam giác đều
  • Tam giác có 3 góc bằng nhau sẽ là tam giác đều
  • Tam giác cân có một góc bằng 60° thì sẽ là tam giác đều
  • Tam giác có 2 góc bằng 60 độ thì sẽ là tam giác đều

Các công thức tam giác đều

Chu vi tam giác đều

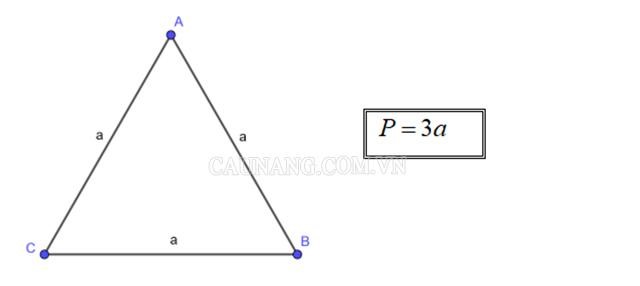
Công thức tính chu vi tam giác đều
Công thức tính chu vi tam giác đều

Công thức tính chu vi của tam giác đều sẽ là: P = 3a.

Trong đó:

  • P: Chu vi
  • a: Độ dài cạnh của tam giác đều

Công thức tính diện tích tam giác đều

Vì tam giác ABC đều nên đường cao kẻ từ đỉnh A sẽ trùng với đường trung tuyến. Diện tích tam giác đều ABC sẽ được tính theo công thức sau:

Xem thêm: Công thức tính thể tích hình lập phương, diện tích và bài tập

Một số bài tập về tam giác đều

Bài tập 1: Cho tam giác ABC đều với cạnh bằng 6cm. Gọi M, N , P lần lượt là trung điểm của cạnh AB, AC, BC. Chứng minh các tam giác AMN, BMP, CNP, MNP đều.

Gợi ý đáp án:

Vì tam giác ABC đều nên , AB = AC = BC

Vì M, N, P lần lượt là trung điểm của AB, AC, BC nên:

AM = MB = AN = NC = BP = PC

Xét tam giác AMN có:

AM = AN

Góc A = 60°

=> Tam giác AMN đều.

Tương tự, ta chứng minh được các tam giác BMP, CNP đều.

Vì ba tam giác AMN, BMP, CNP đều nên MN = MP = PN

=> Tam giác MNP đều.

Xem thêm: Công thức tính diện tích hình bình hành, chu vi và bài tập vận dụng

Bài tập 2: Cho tam giác ABC, có . Chứng minh tam giác đó là tam giác đều.

Gợi ý đáp án:

Xét tam giác ABC có:

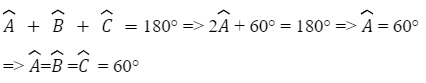
Vậy, tam giác ABC đều.

Với các nội dung thông tin có trong bài viết trên đây, hy vọng sẽ giúp bạn hiểu thêm về khái niệm tam giác đều là gì. Truy cập website caunang.com.vn để tìm hiểu nhiều thông tin hữu ích khác.

Tagged ,